Integrál časové funkce
- Integrování je opačnou matematickou operací než derivování. Také fyzikální podstata integrace je opačná k fyzikální podstatě derivace.
- Derivací časového průběhu kterékoliv fyzikální veličiny jsme získali časový průběh rychlosti změny dané fyzikální veličiny.
- Integrací naopak z časového průběhu rychlosti změny kterékoliv fyzikální veličiny získáme časový průběh dané fyzikální veličiny.
- Pro ilustraci nám opět poslouží vztah mezi dráhou, okamžitou rychlostí a časem.
- Víme, že přírůstek dráhy, vykonaný okamžitou rychlostí za přírůstek času je dán přibližným vztahem:
![]()
- Je zřejmé, že celková dráha vykonaná za určitý čas při nerovnoměrném pohybu je dána součtem všech jednotlivých přírůstků dráhy.
- Pro vyjádření jednotlivých přírůstků dráhy však potřebujeme znát průběh okamžité hodnoty v závislosti na čase.
- Při zvoleném malém konstantním přírůstku času si souhlasně očíslujeme okamžité rychlosti a příslušné přírůstky dráhy. K očíslování použijeme index, který nabývá hodnot 1,2,3 až n. Celkovou dráhu pak pomocí jednotlivých přírůstků vyjadřujeme tímto vztahem:
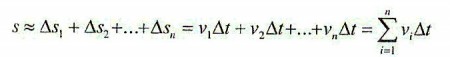
- Na konci výrazu je symbolický zápis jednotlivých součinů. Řecké písmeno sigma zde čteme "suma".
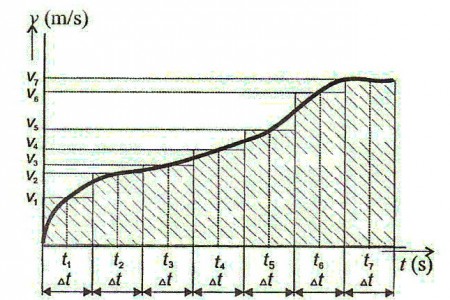
- Využíváme graf časové závislosti rychlosti.
- Každý součin vi . Δt je zde prezentován plochou obdélníku se základnou Δt a výškou určenou příslušnou okamžitou rychlostí vi.
- Celková dráha je pak přibližně dána součtem jednotlivých ploch nacházejících se v časovém intervalu t 1 až t n , ve kterém vykonanou dráhu zjišťujeme. Plochy které jsou pod časovou osou, musíme přičítat se záporným znaménkem, neboť rychlost zde má také záporný smysl.
- Přesnost této metody bude tím větší, čím menší zvolíme časový úsek Δt.
- Grafické integrování:
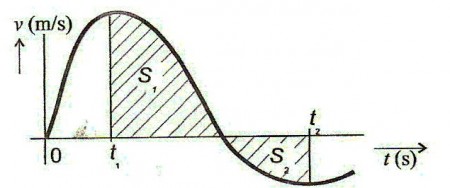
- Geometrickým významem integrálu časové funkce je tedy součet ploch mezi danou funkční křivkou a časovou osou
- Při integrování je někdy zapotřebí uvažovat hodnotu fyzikální veličiny již před integrací, tj. před časem t1.Tuto hodnotu nazýváme počáteční podmínkou integrace.
- V našem případě je počáteční podmínka dána dráhou s0 vykonanou před časem t1.
V našem případě je pomocí integrálu vyjádřena vykonaná dráha takto:
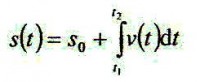
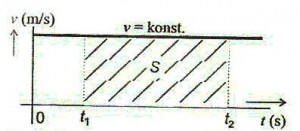
- Na obrázku je vidět, že velikost integrálu konstantní funkce, tj. plochy S pod funkční křivkou (zde přímkou), lineárně roste s dobou integrace, tj. s velkostí integračního intervalu t1 až t2.
- Výraz čteme s(t) se rovná s0 plus integrál od t1 do t2 v(t) dt.
- Diferenciál dt zde vyjadřuje skutečnost, že nezávislou proměnnou, v níž integrace probíhá, je čas.
- Na rozdíl od derivování není integrál konstantní funkce nulový.